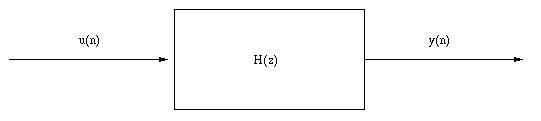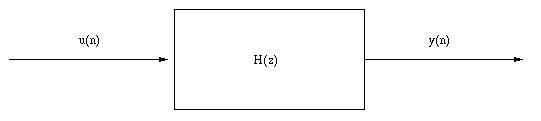Examen de filtrage adaptatif

J.-F. BERCHER

Sans document
Durée : une heure

Questions de cours

  1. Que veut dire LMS ?
  2. Donnez les équations normales (ou de YULE-WALKER) pour l'identification des coefficients d'un filtre à réponse impulsionnelle finie d'ordre p (on ne vous demande pas nécessairement de les démontrer).
  3. Quelles sont les conditions de convergence du LMS ?
  4. Quel est le lien entre l'algorithme du gradient et le LMS ?

Exercice

On considère un filtre autorégressif, de fonction de transfert en z H(z)

ì
ï
ï
í
ï
ï
î
H(z) = a
A(z)
 ,
avec    A(z) = 1+a1z-1+a2 z-2,
excité par un bruit blanc à temps discret u(n), centré et de variance s2 = 1. On note y(n) la sortie de ce filtre.



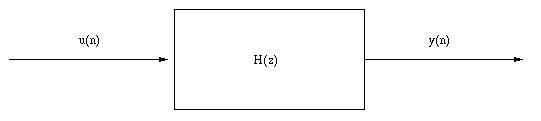
Afin de simplifier le problème, on a choisi a tel que

sY2 = RYY(0) = E{|y(n)|2 } = 1.

Question 1

    1. Donnez l'équation aux différences reliant y(n) et u(n),
    2. déduisez en une relation de récurrence entre RYY(k), RYY(k-1), et RYY(k-2), pour k ³ 1 en notant
      RYY(k) = E{y(n)y(n-k)* },
    3. donnez alors les valeurs de RYY(1) et de RYY(2) en fonction de sY2 , a1 et a2.
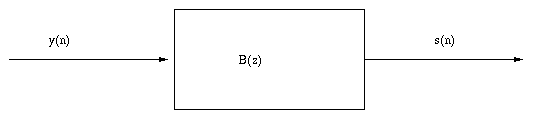
    La sortie y(n est à son tour filtrée, par un filtre adaptatif de fonction de transfert en z

    B(z) = 1 -b1 z-1 - b2 z-2,
    dont le but est de minimiser la variance de la sortie de ce filtre, que l'on notera s(n). L'algorithme utilisé pour adapter les coefficients b1 et b2 est l'algorithme du gradient.



    Question 2

    1. Donnez l'équation aux différences liant s(n) et y(n),
    2. écrivez cette relation en fonction de y(n), du vecteur y(n)t = [y(n-1)     y(n-2)] et du vecteur bt = [b1    b2].
    3. Déduisez en l'expression de la variance de la sortie

      x = E{|s(n)|2 }
      en fonction de b, RYY(0), du vecteur rt = [RYY(1)    RYY(2)] et de la matrice de covariance

      R = é
      ê
      ê
      ê
      ë
      RYY(0)
      RYY(1)
      RYY(1)
      RYY(0)
      		 ù
      ú
      ú
      ú
      û       		.
    4. Donnez le gradient de x,
    5. et déduisez en l'expression de l'algorithme du gradient, qui permet de calculer bn+1 en fonction de bn, en cherchant à minimiser x. Vous noterez m le pas d'adaptation.

    Question 3

    1. Montrez qu'à l'optimum, i.e. pour le vecteur b minimisant x, on a

      E{s(n) y(n) } = E{(y(n) - bty(n))y(n) } = 0.
      (Vous pourrez utiliser pour cela le principe d'orthogonalité, ou le montrer directement).
    2. Comparez le gradient de x à l'expression précédente.
    3. Plutôt que d'utiliser l'expression exacte du gradient (qui fait intervenir la matrice de covariance et le vecteur r inconnus), on utilise les estimées << instantanées >>, c'est-à-dire qu'on supprime l'espérance mathématique des différentes quantités. Que devient alors l'algorithme ?

    Question subsidiaire

    Lorsque l'algorithme a convergé, quelle doit être la sortie s(n) ?

    File translated from TEX by TTH, version 1.0.