Examen de filtrage adaptatif 99

Examen de filtrage adaptatif

J.-F. BERCHER

Tous documents autorisés,
Durée : deux heures.

Les réponses aux questions seront concises, mais précises. Les justifications sont aussi importantes que le résultat brut. Le correcteur appréciera la clarté de la rédaction et de la présentation. Les résultats utiles sont donnés dans le texte (montrez que...) ou dans les questions suivantes... En cas de difficulté sur une question, vous pouvez admettre le résultat, le signaler, et poursuivre.

Il est conseillé de lire attentivement l'énoncé.

Questions de cours

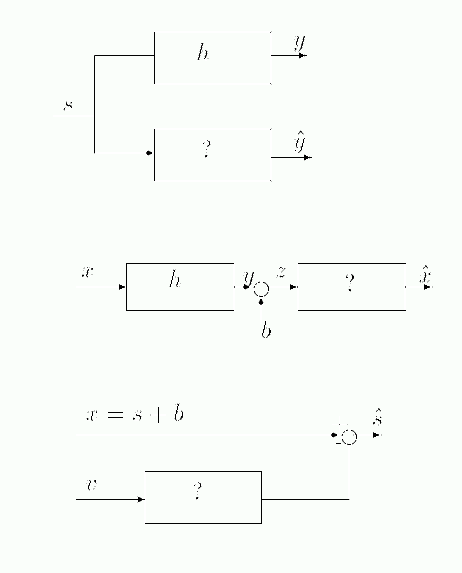
Donnez les équations des filtres de Wiener correspondant aux trois systèmes suivants. Pour chacun d'eux, vous préciserez quel signal est la séquence désirée, quelle est l'erreur d'estimation, et si une séquence d'apprentissage est nécessaire. Expliquez brièvement à quoi peuvent servir ces trois dispositifs.

Exercice : Algorithme LMS normalisé

Dans la forme standard du LMS, la correction mu(n) e(n) appliquée au vecteur [^(w)](n) à l'itération (n+1), est directement proportionnelle à l'entrée u(n). Ainsi, lorsque u(n) est grand, l'algorithme LMS comporte une amplification du bruit e(n). Pour éviter cette difficulté, on peut utiliser l'algorithme LMS normalisé, dans lequel la correction appliquée au vecteur [^(w)](n) à l'itération (n+1), est ``normalisée'' par la norme de u(n) à l'itération n. On s'intéresse dans ce qui suit à la justification de cet algorithme.

Donnez l'expression de l'algorithme LMS habituel. On appelle ``erreur a priori'' l'erreur d'estimation e(n), dont vous préciserez l'expression.
On note e(n) l'erreur a posteriori, obtenue après avoir pris en compte la mesure à l'instant n, u(n) :

e(n) = d(n) - ^
w

(n+1)^t u(n).

Donnez l'expression de e(n) en fonction de e(n), u(n) et de d[^(w)](n+1) = [^(w)](n+1) - [^(w)](n).
Il est raisonnable d'imposer que l'erreur a posteriori soit nulle : e(n) = 0, la nouvelle mesure ayant été prise en compte dans [^(w)](n+1).
1. Montrez que ceci conduit alors à
  
  d ^
  w
  
  (n+1)^t u(n) = e(n).
2. Déduisez de la relation précédente que de manière équivalente,
  
  ^
  w
  
  (n+1)^t u(n) = d(n).
Afin de minimiser les variations [^(w)] d'itération en itération, on choisit de rechercher le vecteur [^(w)](n+1) qui minimise l'écart quadratique à [^(w(n))], tout en imposant la contrainte [^(w)](n+1)^t u(n) = d(n). On recherche donc [^(w)](n+1) tel que

^
w

(n+1) / ě
ď
ď
í
ď
ď
î

min
[^( w)](n+1)
||d ^
w

(n+1)||² =
min
[^( w)](n+1)
[ ^
w

(n+1) - ^
w

(n)]^t [ ^
w

(n+1) - ^
w

(n)]
sous la contrainte ^
w

(n+1)^t u(n) = d(n).

On utilise pour cela la technique des multiplicateurs de Lagrange.

Rappel - Soit le problème de minimisation suivant :

x/ ě
ď
ď
í
ď
ď
î

min
x
F(x)
sous la contrainte G(x) = c,

La solution de ce problème de minimisation sous contraine est fournie par les extrema en x et en l du lagrangien

J(x,l) = F(x) - l(G(x) - c),

où l est un multiplicateur de Lagrange. La technique des multiplicateurs de Lagrange consiste donc (i) à rechercher une solution x (fonction de l) minimisant le lagrangien, i.e. annulant sa dérivée en x, (ii) puis à rechercher la valeur du paramètre de Lagrange en maximisant le lagrangien (en l), ou de manière équivalente, en recherchant la valeur de l qui permet de satisfaire la contrainte G(x) = c.
1. Donnez l'expression du lagrangien associé au problème de minimisation sur [^(w)](n+1).
2. Donnez l'expression de la solution [^(w)](n+1) en fonction de [^(w)](n), u(n) et l.
  
  Rappel - On rappelle que [(d(x- x₀)^t Q(x- x₀))/( dx)] = 2 Q(x- x₀) si Q est une matrice symétrique, et que [(dx^t a)/( dx)] = a.
3. Montrez que la valeur du paramètre de Lagrange permettant de vérifier la contrainte est
  
  l = 2
  ||u(n)||²
  e(n).
4. Finalement, déduisez en que
  
  ^
  w
  
  (n+1) - ^
  w
  
  (n) = 1
  ||u(n)||²
  u(n) e(n).
  
  De manière à contrôler l'écart [^(w)](n+1) - [^(w)](n) sans modifier la direction de descente, on introduit un scalaire [(m)\tilde], tel que
  
  ^
  w
  
  (n+1) - ^
  w
  
  (n) =
  ~
  m
  
  ||u(n)||²
  u(n) e(n).
5. À partir de la relation précédente, donnez l'algorithme LMS normalisé (question ultra-simple), et comparez le à l'algorithme LMS standard.
6. Quels problèmes numériques peuvent apparaître si l'entrée u(n) devient trop faible ou disparait pendant plus de p (longueur de w) échantillons consécutifs ?
En utilisant l'hypothèse d'indépendance entre u(n) et e(n) (fausse), montrez que cet algorithme est convergent en moyenne quadratique si

0 < ~
m

< 2.

Vous pourrez utiliser l'approximation suivante : E{ [(u(n)u(n)^t)/( ||u(n)||²)] } @ [(E{ u(n)u(n)^t })/( E{ ||u(n)||² })], ainsi que le fait que la valeur propre maximale d'une matrice de corrélation R_uu est toujours supérieure ou égale à R_uu(0) = E{ ||u(n)||² }.
L'algorithme LMS est obtenu comme une version stochastique de l'algorithme du gradient déterministe. L'algorithme LMS normalisé peut être vu comme une approximation de l'algorithme du gradient dans lequel on a tenu compte du fait que le pas peut-être variable. L'algorithme du gradient déterministe s'écrit

w(n+1) = w(n) - 1
2
m(n) Ń(n),

avec

Ń(n) = 2[R_uuw(n) - R_du],

où R_uu et R_du respectivement la matrice de corrélation de u(n) et le vecteur d'intercorrélation entre d(n) et u(n).
1. À l'instant (n+1), l'erreur quadratique s'écrit
  
  J(n+1) = E{ ||d(n+1) - w(n+1)^tu(n+1)||² }.
  
  Déterminez la valeur m₀(n) du pas d'adaptation qui minimise J(n+1), en fonction de R_uu et Ń(n) (vous pourrez éventuellement remplacer R_du par son expression en fonction de R_uu et Ń(n), et vous tâcherez de faire apparaître et d'exploiter la différence w(n+1) - w(n)).
2. En utilisant les estimées instantanées de R_uu et Ń(n), déterminez l'estimée instantanée de m₀(n) correspondante. Enfin, donnez l'expression de l'algorithme du gradient stochastique obtenu.